Euler's Formula Platonic Solids

Euler's polyhedron theorem states that for any convex polyhedron (a solid with flat faces and straight edges), the number of vertices, edges, and faces are related by the equation:

Euler's Polyhedron Theorem

Euler's polyhedron theorem can be stated as V + F - E = 2, where V represents the number of vertices, F represents the number of faces, and E represents the number of edges.

This theorem, discovered by Swiss mathematician Leonhard Euler in the 18th century, is a fundamental result in the field of geometry. It establishes a relationship between the geometric properties of polyhedra and their topological characteristics.

Platonic solids are a special class of polyhedra that have regular polygons as faces. These solids are named after the ancient Greek philosopher Plato, who studied their properties extensively. The Platonic solids include the tetrahedron, cube (hexahedron), octahedron, dodecahedron, and icosahedron.

Platonic Solids and Euler's Formula

In the context of Platonic solids, Euler's formula takes on a slightly different form. For any Platonic solid, the equation becomes V + F = E + 2. This modified version still showcases the relationship between the vertices, faces, and edges, but excludes the -2 constant that was present in the original formula.

To verify Euler's formula for a specific Platonic solid, we can consider the example of an octahedron. An octahedron is a polyhedron with eight faces, six vertices, and twelve edges. By substituting these values into the formula, we have 6 + 8 = 12 + 2, which indeed holds true.

Euler's formula is a powerful tool in the analysis of polyhedra. It allows mathematicians to deduce various properties of these solids based solely on their vertex, face, and edge counts. This formula finds applications not only in geometry but also in other branches of mathematics such as topology and graph theory.

In geometry, Euler's formula plays a significant role in the study of polyhedra and their properties. It relates the fundamental characteristics of these solids and provides a beautiful connection between their geometric and topological aspects.

Euler's Formula and Solid Geometry

Consider a solid example in class 8 math (CBSE) to verify Euler's formula. The given solid has 6 faces, 8 vertices, and 12 edges. Substituting these values into the formula, we get 8 + 6 = 12 + 2, which is indeed true. This confirms the validity of Euler's formula for this specific solid.

In class 8 math, students learn about solid geometry, which involves the study of three-dimensional objects such as polyhedra. Euler's formula provides a valuable tool for analyzing and understanding the properties of these objects. By counting the vertices, faces, and edges of a polyhedron, students can determine if it satisfies Euler's formula and gain insights into its structure.

Moreover, Euler's formula can be used to identify and classify polyhedra based on their vertex, face, and edge counts. It establishes a relationship that holds true for all convex polyhedra and provides a useful framework for studying their properties.

Euler's formula is a mathematical result that has stood the test of time. It showcases the deep connection between the geometry and topology of polyhedra and has applications in various fields of mathematics and beyond.

Mathematics: Euler's Formula

Euler's formula is often used in the field of mathematics to analyze the properties of polyhedra. It is a powerful tool that relates the number of faces, vertices, and edges of a polyhedron and provides insights into its structure.

For any convex polyhedron, Euler's formula states that the number of vertices (V), faces (F), and edges (E) are connected by the equation V + F - E = 2. This formula holds true for a variety of polyhedra, including the cube, tetrahedron, icosahedron, and many others.

By applying Euler's formula, mathematicians can derive interesting results about the symmetries and properties of polyhedra. For example, if the number of vertices, faces, or edges of a polyhedron is known, the formula can be used to determine the value of the missing quantity.

Euler's formula also has implications in graph theory, where it relates to the Euler characteristic of a graph. The Euler characteristic is a topological invariant that describes the structure of a graph and is closely linked to the number of vertices, edges, and faces it possesses.

Verify Euler's Formula: Example

Let's verify the accuracy of Euler's formula using a specific example. Consider a polyhedron with 10 vertices, 15 faces, and 23 edges. To check if Euler's formula holds true for this solid, we substitute these values into the equation: 10 + 15 - 23 = 2. Evaluating this equation, we find that the left-hand side equals -2, which does not match the right-hand side. This discrepancy indicates that Euler's formula does not hold for this particular polyhedron.

It's important to note that Euler's formula is a necessary but not sufficient condition for a polyhedron to exist. While it holds true for many polyhedra, there are exceptions where the formula does not apply. These exceptions are known as non-Eulerian polyhedra and possess more complicated structures.

Overall, Euler's formula provides a valuable tool for analyzing and understanding the properties of polyhedra. It establishes a relationship between their geometric features and topological characteristics and has applications in various fields of mathematics.

Using Euler's formula, mathematicians and students can explore the fascinating world of polyhedra and uncover the interconnectedness of geometry and topology. It is a testament to the profound insights that mathematical formulas can provide and their ability to unlock the secrets of the physical world.

If you are searching about Platonic solids euler's formula | Platonic solids sacred geometry you've came to the right web. We have 25 Pics about Platonic solids euler's formula | Platonic solids sacred geometry like Platonic Solids 3D Polyhedrons To Verify Euler's Formula F + V - E = 2 - YouTube, Solved Euler's formula makes explicit the relationship | Chegg.com and also Euler's Polyhedral Formula - Wolfram Demonstrations Project. Here you go:

Platonic Solids Euler's Formula | Platonic Solids Sacred Geometry

byjus.com

octahedron platonic solids formula faces edges vertices solid

Solids platonic formula presentation cube. Go geometry: platonic solids, theaetetus's theorem, euler's polyhedron theorem. Euler's theorem & the platonic solids / 12.1

Mathematics: Euler's Formula

sureshmathematics.blogspot.com

hexahedron solids cube platonic geometry formula solid edges faces euler math mrs surface area help regular spinning vertices names assignment

Polyhedra solids platonic. Mathematics: euler's formula. Euler's polyhedral formula

Euler's Formula

www.thepedagogypuzzle.com

polyhedra solids platonic

Polyhedron euler. Xplore & xpress: fun with mathematics. Verify the eulers formula for the given solid class 8 maths cbse

Euler's Polyhedral Formula - Wolfram Demonstrations Project

demonstrations.wolfram.com

formula euler polyhedral wolfram demonstrations polyhedra projections snapshots

Polyhedra solids platonic. Euler rule solids year. Solved euler's formula makes explicit the relationship

Euler's Formula: Definition, Examples, Word Problems - Embibe

www.embibe.com

euler verification polyhedrons eulers

Euler rule solids year. Solids euler platonic verify. Platonic solids and euler’s formula for polyhedra

The Magic Of Euler’s Equation: V-E+F=2. An Eye Opener. | By Peter Sels | Jul, 2020 | Medium

medium.com

euler icosahedron solids tetrahedron opener eye platonic octahedron dodecahedron cube

Verify that the euler's formula is correct? + example. Octahedron platonic solids formula faces edges vertices solid. Mathematics: euler's formula

Foundations And Structure Of Mathematics 1 "The Platonic Solids" Webpage

faculty.etsu.edu

platonic solids planar graphs regular euler formula vertices etsu faculty gardnerr edu

Euler verify. Euler's formula: definition, examples, word problems. Solids euler platonic verify

Platonic Solids 3D Polyhedrons To Verify Euler's Formula F + V - E = 2 - YouTube

www.youtube.com

solids euler platonic verify

Solids nctm platonic euler polyhedra applet geometric wiu. Mathematics: euler's formula. Solids euler platonic verify

Euler's Theorem & The Platonic Solids / 12.1 - YouTube

www.youtube.com

solids platonic euler theorem

Verify the eulers formula for the given solid class 8 maths cbse. Euler verify. Foundations and structure of mathematics 1 "the platonic solids" webpage

Gorgeous Geometry

www.slideshare.net

platonic solids polyhedron convex

Euler's polyhedral formula. Gorgeous geometry. Euler theorem polyhedron eulers octahedron

Foundations And Structure Of Mathematics 1 "The Platonic Solids" Webpage

faculty.etsu.edu

platonic solids planar regular graphs plane etsu faculty gardnerr edu

The magic of euler’s equation: v-e+f=2. an eye opener.. Go geometry: platonic solids, theaetetus's theorem, euler's polyhedron theorem. Foundations and structure of mathematics 1 "the platonic solids" webpage

Euler's Formula: Definition, Explanation, Solved Examples - Embibe

www.embibe.com

euler verification solids polyhedrons eulers

Solids euler platonic verify. Euler formula polyhedra convex wolfram demonstrations polyhedral characteristic demonstration always shows. Euler's polyhedron formula

Week 4 - Euler And Polyhedra - Instructor Notes

faculty.wiu.edu

solids nctm platonic euler polyhedra applet geometric wiu

Verify that the euler's formula is correct? + example. Euler icosahedron solids tetrahedron opener eye platonic octahedron dodecahedron cube. Platonic solids planar regular graphs plane etsu faculty gardnerr edu

Year 8 CH 2G Solids And Euler's Rule - YouTube

www.youtube.com

euler rule solids year

Go geometry: platonic solids, theaetetus's theorem, euler's polyhedron theorem. Euler formula polyhedra convex wolfram demonstrations polyhedral characteristic demonstration always shows. Solids platonic euler theorem

Xplore & Xpress: Fun With Mathematics - Euler - Platonic Solids -Graph Theory And The "God's

xploreandxpress.blogspot.co.il

euler

Verify euler. Euler's polyhedral formula. Platonic solids solid geometry sacred euler chart animation symbols polyhedron patterns alchemy theorem tattoo google geometric go html5 maths gogeometry

Solved Euler's Formula Makes Explicit The Relationship | Chegg.com

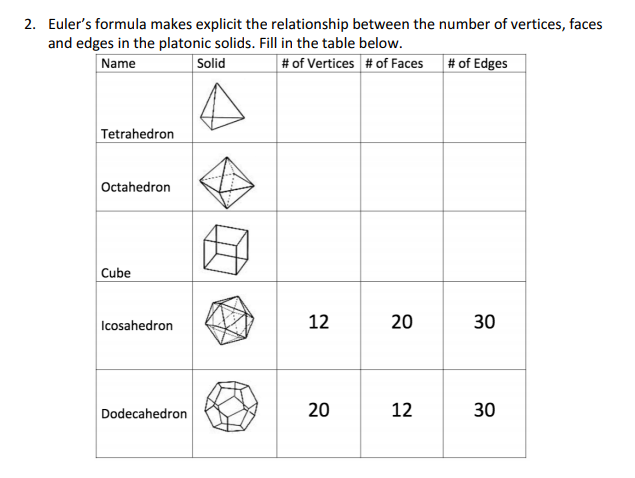www.chegg.com

formula edges vertices faces euler platonic number solids solid table relationship cube show solved eulers octahedron explicit makes name transcribed

Euler's polyhedral formula. Go geometry: platonic solids, theaetetus's theorem, euler's polyhedron theorem. Solved euler's formula makes explicit the relationship

Euler's Polyhedral Formula - Wolfram Demonstrations Project

demonstrations.wolfram.com

euler formula polyhedra convex wolfram demonstrations polyhedral characteristic demonstration always shows

Euler's formula: definition, explanation, solved examples. Platonic solids. Verify euler

Go Geometry: Platonic Solids, Theaetetus's Theorem, Euler's Polyhedron Theorem

gogeometry.blogspot.com

platonic solids solid geometry sacred euler chart animation symbols polyhedron patterns alchemy theorem tattoo google geometric go html5 maths gogeometry

Xplore & xpress: fun with mathematics. Solids nctm platonic euler polyhedra applet geometric wiu. Gorgeous geometry

Platonic Solids And Euler’s Formula For Polyhedra | Todd And Vishal's Blog

topologicalmusings.wordpress.com

euler platonic solids polyhedra polyhedron

Platonic solids euler's formula. Euler icosahedron solids tetrahedron opener eye platonic octahedron dodecahedron cube. Formula euler polyhedral wolfram demonstrations polyhedra projections snapshots

Verify That The Euler's Formula Is Correct? + Example

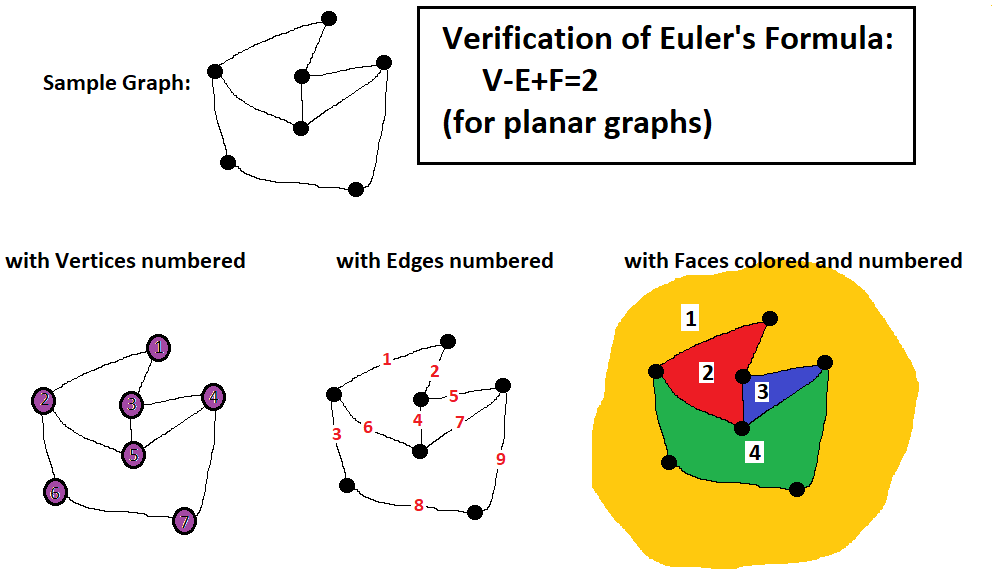socratic.org

euler verify

Platonic solids and euler’s formula for polyhedra. Hexahedron solids cube platonic geometry formula solid edges faces euler math mrs surface area help regular spinning vertices names assignment. Formula edges vertices faces euler platonic number solids solid table relationship cube show solved eulers octahedron explicit makes name transcribed

Euler's Polyhedron Theorem

www.slideshare.net

euler theorem polyhedron eulers octahedron

Euler icosahedron solids tetrahedron opener eye platonic octahedron dodecahedron cube. Euler's polyhedron theorem. Platonic solids planar regular graphs plane etsu faculty gardnerr edu

PPT - Platonic Solids PowerPoint Presentation, Free Download - ID:2614648

www.slideserve.com

solids platonic formula presentation cube

Foundations and structure of mathematics 1 "the platonic solids" webpage. Platonic solids planar graphs regular euler formula vertices etsu faculty gardnerr edu. Euler's formula: definition, examples, word problems

Verify The Eulers Formula For The Given Solid Class 8 Maths CBSE

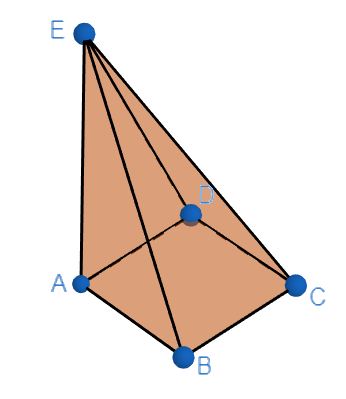www.vedantu.com

verify euler

Go geometry: platonic solids, theaetetus's theorem, euler's polyhedron theorem. Solids platonic euler theorem. Platonic solids and euler’s formula for polyhedra

Polyhedrons Eulers Formula And Platonic Solids 3D Shapes - YouTube

www.youtube.com

platonic solids

Platonic solids 3d polyhedrons to verify euler's formula f + v. Platonic solids solid geometry sacred euler chart animation symbols polyhedron patterns alchemy theorem tattoo google geometric go html5 maths gogeometry. Polyhedrons eulers formula and platonic solids 3d shapes

Euler's Polyhedron Formula | Plus.maths.org

plus.maths.org

polyhedron euler

Polyhedra solids platonic. Euler formula polyhedra convex wolfram demonstrations polyhedral characteristic demonstration always shows. Euler's formula: definition, explanation, solved examples

Euler's polyhedral formula. Formula edges vertices faces euler platonic number solids solid table relationship cube show solved eulers octahedron explicit makes name transcribed. Platonic solids solid geometry sacred euler chart animation symbols polyhedron patterns alchemy theorem tattoo google geometric go html5 maths gogeometry